Rolle’s Theorem

Rolle's Mean Value Theorem

In calculus, there exists a theorem that guarantees the existence of a point where the slope of the tangent is zero if a function starts and ends at the same value on an interval. This result is known as Rolle’s Theorem. It is one of the core theorems in differential calculus.

$$\text{Rolle's Theorem Graph}$$

Formula used for Rolle's Theorem:

$$f'(c) = 0$$

Statement

A function $f$ is defined in the closed interval $[a, b]$ in such a way that it satisfies the following condition:

1. $f(x)$ is continuous in the closed interval $a \leq x \leq b$
2. $f(x)$ is differentiable in the open interval $a < x < b$
3. $f(a) = f(b)$ Then, there exists at least one point $'c'$ in the open interval $(a, b)$ such that:

$$f'(c) = 0$$

Geometric Interpretation of Rolle’s Theorem

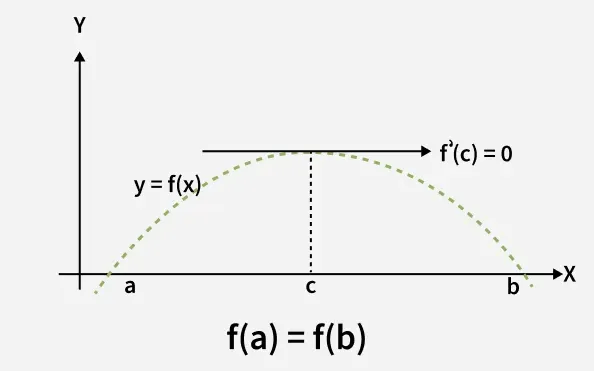
We can visualize Rolle's theorem from the figure(1) added below,

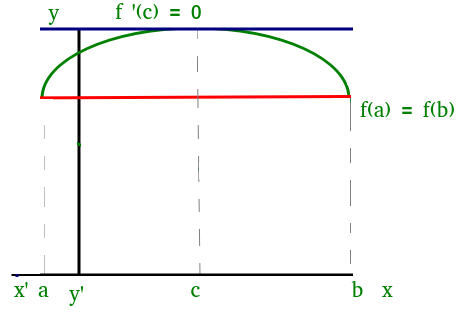
In the above figure the function satisfies all three conditions given above. So, we can apply Rolle's theorem, according to which there exists at least one point $'c'$ such that:

$$f'(c) = 0$$

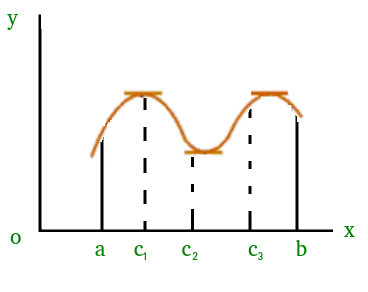
which means that there exists a point at which the slope of the tangent at that is equal to 0. We can easily see that at point $'c'$ slope is 0. Similarly, there could be more than one points at which slope of tangent at those points will be 0. Figure(2) added below is one of the example where exists more than one point satisfying Rolle's theorem.

Proof of Rolle's Mean Value Theorem

Consider a function $f$ that satisfies the conditions of Rolle's Theorem:

Since $f$ is continuous on $[a,b]$ and differentiable on $(a,b)$ by the Extreme Value Theorem, $f$ attains its maximum and minimum values on $[a,b]$. If the maximum or minimum value is attained at some point $c$ in $(a,b)$, then $f'(c)=0$ since the tangent line at $c$ is horizontal. If the maximum and minimum values are attained at the endpoints $a$ or $b$, then $f$ is constant on $[a,b]$ and $f'(x)=0$ for all $x$ in $(a,b)$.

Therefore, there exists at least one point $c$ in $(a,b)$ such that $f'(c) = 0$.

Related Articles:

• Mean Value Theorem
• Rolle's Theorem and Lagrange's Mean Value Theorem
• Lagrange's Mean Value Theorem
• Rolle’s Mean Value Theorem

Applications of Rolle's Mean Value Theorem in CS

Various applications of Rolle's Mean Value theorem in CS field:

• Algorithm Correctness: In analyzing functions used in algorithms, Rolle’s theorem guarantees the existence of critical points (where derivative = 0), important in optimization and proving algorithm stability.
• Signal Processing: When signals start and end at the same value, Rolle’s theorem ensures that somewhere in between the rate of change of the signal is zero (flat point), useful in compression and smoothing.
• Computer Graphics & Animation: While designing curves that begin and end at the same height, Rolle’s theorem ensures there will be at least one point of horizontal tangent, useful for smooth rendering.

Solved Examples on Rolle's Theorem

Example 1: Verify Rolle’s theorem for function $y = x^2 + 4$, $a = –1$ and $b = 1$.

Solution: Given function $y = x^2 + 4$, as it is a polynomial function, is continuous in $[– 1, 1]$ and differentiable in $(–1, 1)$. Also,

$f(-1) = (-1)^2 + 4 = 1 + 4 = 5$

$f(1) = (1)^2 + 4 = 1 + 4 = 5$

Thus, $f(– 1) = f(1) = 5$

Hence, the function $f(x)$ satisfies all conditions of Rolle's theorem.

Now, $f'(x) = 2x$

Rolle’s theorem states that there is a point $c \in (– 1, 1)$ such that $f'(c) = 0.$

$2c = 0$

$c = 0, where c = 0 \in (–1, 1)$

Example 2: Verify Rolle’s theorem for function $y = 2x + 8$, $a = –1$ and $b = 1$.

Solution:

Given function $y = 2x + 8$, as it is a polynomial function, is continuous in $[– 1, 1]$ and differentiable in $(–1, 1)$. Also,

$f(-1) = 2(-1) + 8 = -2 + 8 = -6$

$f(1) = 2(1) + 8 = 2 + 8 = 10$

Thus, $f(– 1) ≠ f(1)$

Hence, Rolle's theorem is not applicable.

Example 3: Verify Rolle's theorem for $f(x) = 3x - 2$, $a = 0$ and $b = 2.$

Solution:

$f(x) = 3x - 2$ is a polynomial, so it's continuous on $[0, 2]$ and differentiable on $(0, 2)$.

$f(0) = 3(0) - 2 = -2$

$f(2) = 3(2) - 2 = 4$

Thus, $f(0) ≠ f(2)$

Hence, Rolle's theorem is not applicable.

Example 4: Verify Rolle's theorem for $f(x) = x² + 1$, $a = -2$ and $b = 2.$

Solution:

$f(x) = x² + 1$ is a polynomial, so it's continuous on $[-2, 2]$ and differentiable on $(-2, 2)$.

$f(-2) = (-2)² + 1 = 5$

$f(2) = (2)² + 1 = 5$

Thus, $f(-2) = f(2)$

Rolle's theorem is applicable. ($c = 0$ where $f'(c) = 0$)

Example 5: Verify Rolle's theorem for $f(x) = |x|$, $a = -1$ and $b = 1.$

Solution:

$f(x) = |x|$ is continuous on $[-1, 1]$, but not differentiable at $x = 0.$

$f(-1) = |-1| = 1$

$f(1) = |1| = 1$

Thus, $f(-1) = f(1)$

However, $f(x)$ is not differentiable on the entire open interval $(-1, 1)$.

Hence, Rolle's theorem is not applicable.

Example 6: Verify Rolle's theorem for $f(x) = e^x$, $a = 0$ and $b = \ln(2)$.

Solution:

$f(x) = e^x$ is continuous and differentiable everywhere.

$f(0) = e^0 = 1$

$f(\ln(2)) = e^{\ln(2)} = 2$

Thus, $f(0) ≠ f(\ln(2))$

Hence, Rolle's theorem is not applicable.

Example 7: Verify Rolle's theorem for $f(x) = \cos(x)$, $a = 0$ and $b = 2\pi.$

Solution:

$f(x) = \cos(x)$ is continuous and differentiable everywhere.

$f(0) = \cos(0) = 1$

$f(2\pi) = \cos(2\pi) = 1$

Thus, $f(0) = f(2\pi)$

Rolle's theorem is applicable. ($c = \pi$ where $f'(c) = 0$)

Example 8: Verify Rolle's theorem for $f(x) = x^3 - x$, $a = -1$ and $b = 1.$

Solution:

$f(x) = x^3 - x$ is a polynomial, so it's continuous on $[-1, 1]$ and differentiable on $(-1, 1).$

$f(-1) = (-1)^3 - (-1) = -1 + 1 = 0$

$f(1) = (1)^3 - (1) = 1 - 1 = 0$

Thus, $f(-1) = f(1) = 0$

Rolle's theorem is applicable. ($c = 0, ±\frac{1}{\sqrt{3}}$ where $f'(c) = 0$)

Example 9: Verify Rolle's theorem for $f(x) = \frac{1}{x}$, $a = 1$ and $b = 2.$

Solution:

$f(x) = \frac{1}{x}$ is continuous and differentiable for $x > 0$, so it's continuous on $[1, 2]$ and differentiable on $(1, 2).$

$f(1) = \frac{1}{1} = 1$

$f(2) = \frac{1}{2} = 0.5$

Thus, $f(1) ≠ f(2)$

Hence, Rolle's theorem is not applicable.

Example 10: Verify Rolle's theorem for $f(x) = \sin(x)$, $a = 0$ and $b = \pi.$

Solution:

$f(x) = \sin(x)$ is continuous and differentiable everywhere.

$f(0) = \sin(0) = 0$

$f(\pi) = \sin(\pi) = 0$

Thus, $f(0) = f(\pi) = 0$

Rolle's theorem is applicable. ($c = \frac{\pi}{2}$ where $f'(c) = 0$)

Practice Problems on Rolle's Mean Value Theorem

Question 1: Verify Rolle's theorem for $f(x) = x^2 - 4x + 3$ on the interval $[1, 3].$

Question 2: Check if Rolle's theorem applies to $f(x) = e^x$ on $[0, \ln(2)].$

Question 3: Determine whether Rolle's theorem can be applied to $f(x) = |x|$ on $[-2, 2].$

Question 4: Verify Rolle's theorem for $f(x) = \sin(x)$ on $[0, 2\pi].$

Question 5: Examine if Rolle's theorem is applicable for $f(x) = \frac{1}{x^2+1}$ on $[-1, 1].$

Question 6: Check the applicability of Rolle's theorem for $f(x) = x^3 - 3x$ on $[-\sqrt{3}, \sqrt{3}].$

Question 7: Verify if Rolle's theorem can be applied to $f(x) = \ln(x^2)$ on $[-e, e].$

Question 8: Determine if Rolle's theorem holds for $f(x) = \cos^2(x)$ on $[0, \pi].$

Question 9: Check whether Rolle's theorem is applicable to $f(x) = x^4 - 5x^2 + 4$ on $[-1, 1].$

Question 10: Verify if Rolle's theorem can be applied to $f(x) = \tan(x)$ on $[0, \pi].$